

|
This puzzle is built on a 4 sided right triangle decaflexagon, with 10 triangles per face arranged as a pentagon. One of the interesting things about this flexagon is that there are flexes that affect less than half of it. This allows for a puzzle where you can figure out a series of flexes to help you solve it. There are four loops to find in this puzzle. Click on following pictures to get the full sized version. 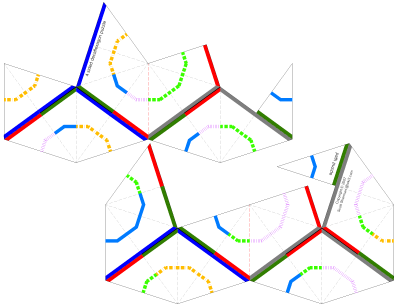
Cut out the two shapes. Fold them in half along the dashed red lines in the center and paste the halves together. Once dry, cut along the four thick black lines. Pre-crease along all the gray dashed lines. There should be two triangles with the word “puzzle” on them. Paste these two back to back to connect the two pieces. You should now have something that looks like this. 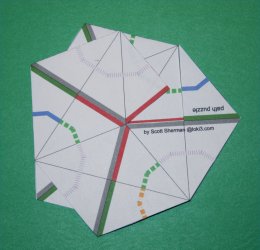
You’ll do the final folding of the flexagon based on the colors along the short edges of the triangles. First fold the adjacent gray triangles together followed by the adjacent green triangles. The easiest method is to alternate gray and green. When finished, you should have a pentagon with a red border on one side and blue border on the other. Paste the final two overlapping triangles together (or tape them if you want the option of being able to take it apart and re-fold it if you get lost flexing). Once dry, fold the flexagon in half in various ways to get it ready for flexing. 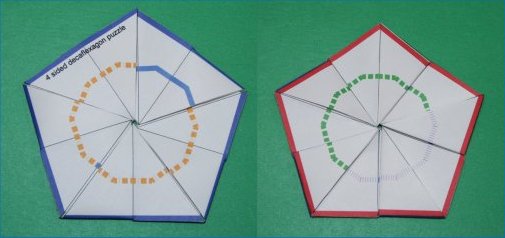
You should see one side with an entirely red border and one side with a blue border. The colored paths in the middle are mixed up. The puzzle is to see each of the four paths in its entirety. The “silver tetra flex”One flex that can help you solve the puzzle is also the main flex for the 45-45-90 triangle (aka silver triangle) tetraflexagon. On the decaflexagon, you can perform this on 4 of the 10 triangles on a face at a time, allowing you to rearrange just part of the flexagon. This can allow you to pick four adjacent triangles you want to change without affecting anything else. Look at the side with the red border and note that there are 6 triangles with a green path of boxes and 4 triangles with a path of purple lines. To solve the green path, fold it in half through the middle of the green path and the purple path, with the purple lines facing to the left. 
Hold onto the six triangles with the green path while pushing the left tip down. The four triangles with the purple lines should open up on both sides into a pyramid-like shape, allowing you to push the tip all the way down. 
Now open up the top point of the pyramid into an inverted pyramid shape and pull the tip all the way down till the flexagon lies flat again. 
The two triangles on the left should flip up, revealing four triangles with gray along their edges. 
Fold the left two triangles backwards until the flexagon is flat. You should now be able to unfold it back into a pentagon. The green path will now be complete while several of the borders have changed from red to gray. 
You can perform this flex in reverse to restore it to its original state. It’s useful to practice this flex in both directions to help you solve the other three paths. This flex sequence will swap four adjacent triangles, though you may not be able to perform the flex in all places when the flexagon has been mixed up. The red and gray sides will trade triangles and the blue and green sides will swap triangles. With this knowledge, you should be able to solve the gold path of squares and lines. Other flexesIn order to solve the purple path and the solid blue path, you’ll need another type of flex sequence in addition to the silver tetra flex. There are many different flexes that’ll help - a pinch flex involving the entire flexagon, a flex that only involves 6 of the 10 triangles. Have fun experimenting and exploring this flexagon! More information on the decaflexagon |
