|
The triangle tetraflexagon has 4 triangles meeting in the center. Note that the term tetraflexagon is often used for flexagons with 4 squares meeting in the center, therefore I'll always qualify my usage of the term with triangle, silver or equilateral. Three variants are described here:
The equliateral triangle tetraflexagon is sometimes called a flexacup or pyramid flexagon. 
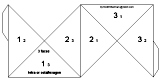
The following video shows an interesting illusion on a silver tetraflexagon. You can find a template for making it at Silver Tetraflexagon Illusion page. Silver TetraflexagonFour triangles meet in the center of a triangle tetraflexagon, so if you want it to lie flat, you should use right triangles. An obvious selection is a 45-45-90 (silver) triangle. This will give you a square when the 90 degree angles are in the middle. To flex, fold it in half diagonally then open it along the bottom of the longest edge of the triangle giving you a small square. Open this at the vertex opposite the one you closed and itíll open up to a triangle. Open this up at the tip and youíll arrive at another full square with four triangles meeting in the center. Note that you wonít always be able to travel through this entire sequence. A single copy of this first net gives you a silver tetraflexagon while two copies gives you an octaflexagon. Cut out the net and pre-crease all the edges. Copy the small numbers on to the back. To fold the 3 sided silver tetraflexagon, fold the adjacent 2ís together then slip one end under the other so the other pair of 2ís face each other. Tape the tabs onto the appropriate faces. This should give you a square with four 1ís on one side and 4 3ís on the other. There are a couple flexings that will reveal the 2 face but you canít open it up.
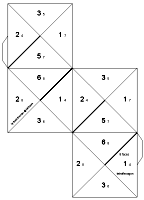
To fold the 8 sided version, fold 8 on 8, 7 on 7, 6 on 6, 5 on 5 and 3 on 3. Now fold the adjacent 4ís together and tuck one end under the other so the other pair of 4ís face each other. You should be able to get faces 1, 2, 7 and 8 to lie flat. The other faces can be seen on the inside as you flex between states.
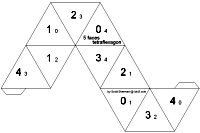
Equilateral Triangle TetraflexagonAnother possible triangle tetraflexagon uses equilateral triangles. Since 4x60 < 360, this one never opens flat. In fact, as you flex it the same side will always be on the outside. But youíll see the inside number change as you flex. Start by folding the 1ís onto the adjacent 1ís. Fold the adjacent 2ís together then the adjacent 3ís. This will leave you with 0ís on one side and 4ís on the other. Fold it in half and tape the tabs onto the appropriate faces. This should leave you with 0ís on the outside. You should be able to open up one corner and see 4ís or the other corner to see 3ís. If you open up the 3ís, keep flexing until you fold it in half the other way. You can then open up the opposite corner to see the 2ís.
One way to create others of this variety is to start from any hexaflexagon strip and use two copies of the pattern instead of three. Due to the nature of this flexagon, however, you probably wonít be able to reach all the sides. To derive a more optimal strip, simply paste together the sides you canít get to. Star Triangle Tetraflexagon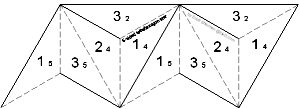
Cut along the solid lines and pre-fold along the dashed lines. The dashed lines along the outside edge of triangles 1/5 indicate that this edge will be connected to another edge. Copy the small numbers onto the backs of the triangles. Tape together the dashed edge of 1/5 to the short edge of 3/2 such that 1 and 2 are on the same side and 3 and 5 are on the same side. Fold adjacent 5's on top of each other and adjacent 4's on top of each other. This may require a bit of twisting. Fold together the single pair of adjacent 3's. One side should now have four 1's and a 3 while the other side has four 2's and a 3. Fold the middle pair of 2's together and finish by folding the adjacent 3's together. Tape the dashed edge of 1/5 to the short edge of the 3/2 below it. You can now use the pivot flex to reveal side 4. If you pivot back to side 1, you can open up the inside (with 2's) to make a diamond. Open up the other side (with 3's on the inside) then do another pivot to get to side 5. Next: The Pentaflexagon |