12 leaf hexaflexagon
|
This flexagon has lots of symmetry and interesting patterns. It has 36 different states, where half the leaves are visible at a time. This means that the leaves get pretty jumbled as you wander around it. To help make sense of all these states, I've decorated it with a series of rings. The rings vary by size, color and linetype. FoldingTo make this hexaflexagon, click on each of the following two thumbnails to get a larger version. If you print the two strips back-to-back, with like numbers opposite each other, the model will be easier to flex. Or you may choose to print them out separately and paste them together, which may be easier to construct. Once printed, pre-crease along the dashed gray lines. Start with 0* on the top. Fold 2 under 1, 5 under 4, then 7 on 6. Fold 7 on 4, then 8 under 5. Finish by folding 11 under 10 and taping the edges of 0 and 11 together. 

Understanding the cyclesThe video above shows several cycles that modify one or more attributes of the rings. Below I give more detail on exactly what these cycles are. For more information on the notation used for describing the flex sequences, see flex notation. This first cycle is a series of pinch flexes. The ring number and linetype stay the same, while the colors cycle. 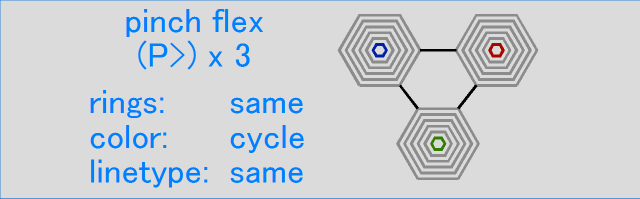
This particular combination of the tuck, inverse tuck and pyramid shuffle is called the S-cycle. Both the colors and linetype stay the same, but the ring number cycles. 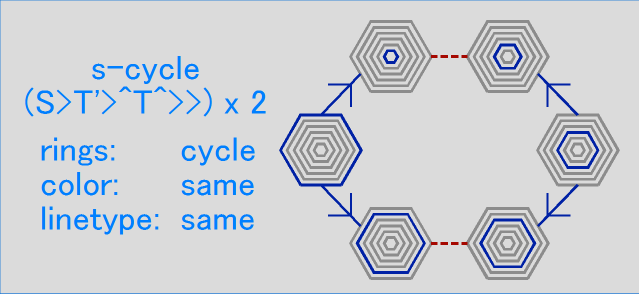
The v-flex cycles the ring number and color at the same time, while leaving the linetype untouched. 6 v-flexes bring you back to the start of the cycle. 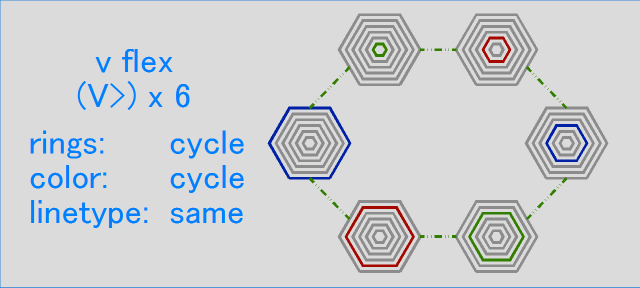
The slot-tuck flex is the only one of the flexes here that changes the linetype. It cycles through ring numbers as well, though not in order. The color stays the same. 
The flex sequence (LtP'<P'<) x 12 allows you to cycle through all 36 states exactly once. The flex sequence (LtT'^<T^) x 12 also cycles through all 36 states exactly once. ExploringThe following diagram shows how you can travel between any of the 36 states using the pinch flex, v-flex, tuck flex, pyramid shuffle, and slot-tuck flex. The legend along the right side shows how to interpret the labels for each state. The number indicates which of the 6 rings is complete for that state. The letter represents the pair of colors of the two sides in the state, e.g. 'a' indicates that there's a complete blue ring on one side and red ring on the other. The linetype differentiates the inner three hexagons from the outer three hexagons. State 1a and 1a' share all the same leaves that have solid lines on the leaves, but state 1a has dashed rectangles on the leaves that are unique to it, while state 1a' has dashed lines on the leaves that are unique to it. 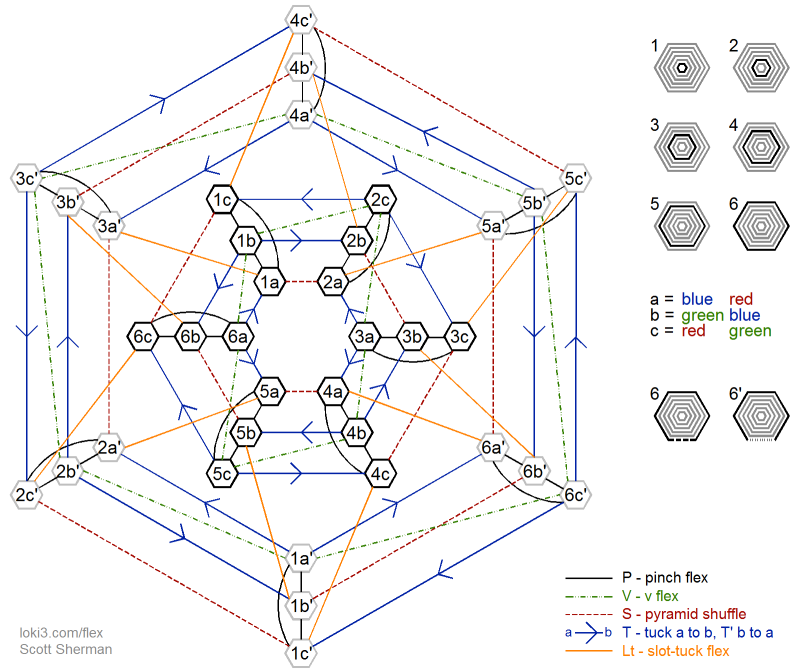
The following version of the diagram shows just the v-flexes, tuck flexes and pyramid shuffles. You can see the 6 hexagon rings that represent the S-cycle of (S>T'>^T^>>) x 2. The v-flex ties some of the rings together, but there isn't a way to get from the inner 3 rings to the outer 3 rings using just these flexes. Adding the pinch flex wouldn't help either. 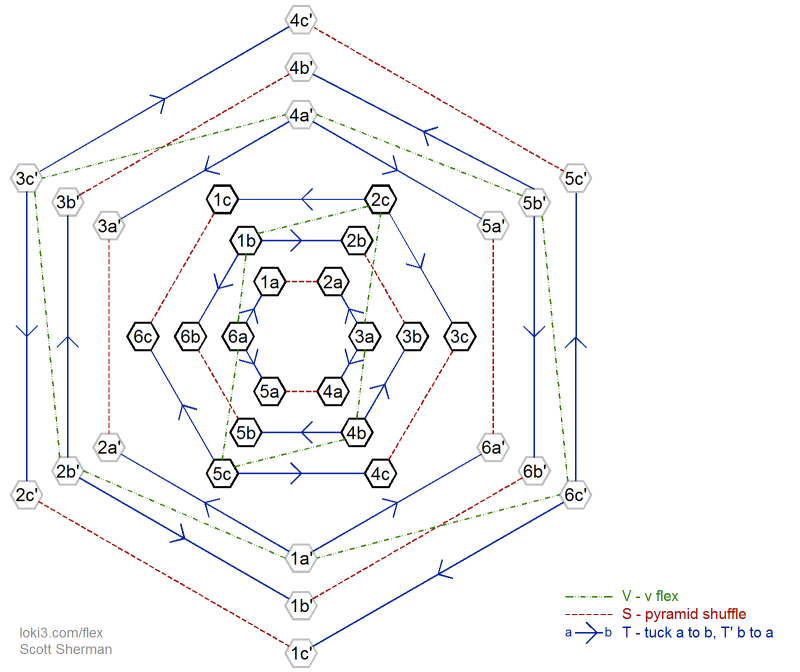
The next version of the diagram shows just the pinch flexes and slot-tuck flexes. As you can see, with just these two flexes you can traverse all 36 states. In fact, it also suggests a simple way to traverse all the states. Using the flex sequence (LtP'<P'<) x 12, you can visit each state exactly once. 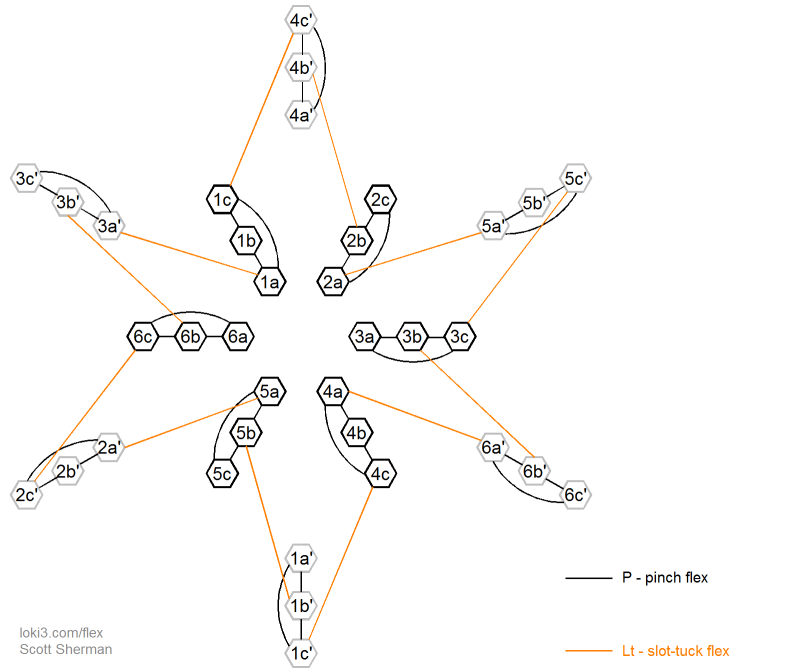
The next diagram shows that you can also traverse all states using the flex sequence (LtT'^<T^) x 12. 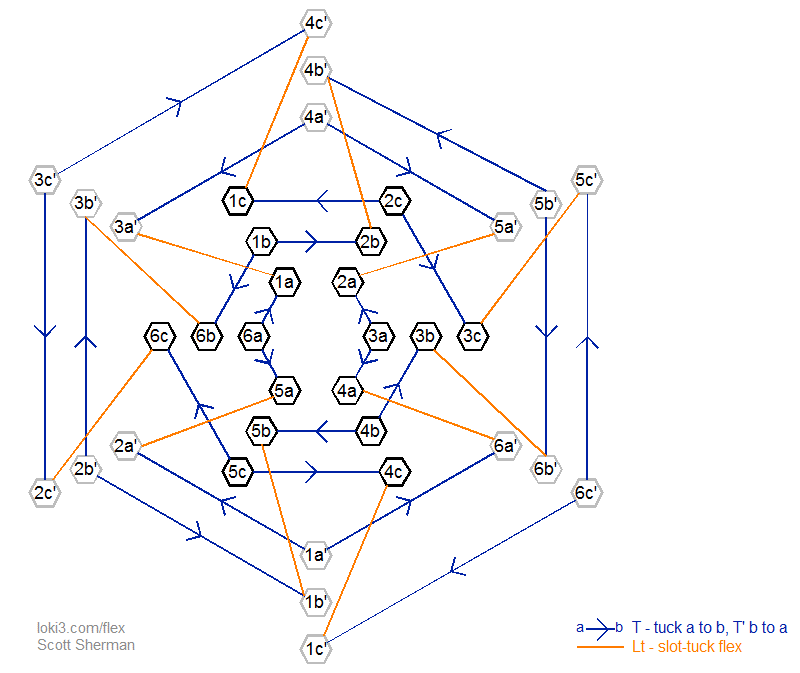
The final diagram describes each of the sides on the inner three hexagons and shows where to perform each flex and which state the flex leads to. The outer three hexagons have similar behavior. 
|
