|
The hexaflexagon has 6 triangles meeting in the center. Three variants are described here:
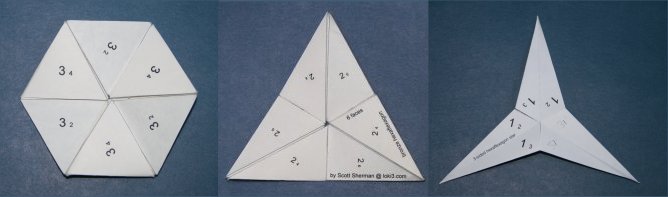
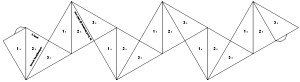
Equilateral Triangle HexaflexagonIf someone knows something about flexagons, they most likely know the hexaflexagon made out of equilateral triangles. It was the first flexagon discovered and is the most popular variety. While many people have written about it before, few have explored the rich variety of flexes you can perfrom on it. The common flex people describe is called the pinch flex and sometimes you can find reference to the v-flex. Much less well known are the slot flex, pocket flex, pyramid shuffle, and tuck flex. The following video demonstrates these flexes. 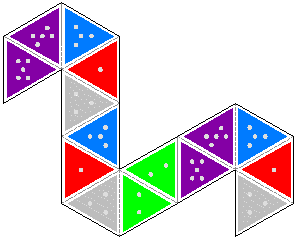One type of strip used in making equilateral triangle hexaflexagons is called a braid. Braids happen to be the only way to make an equilateral triangle tetraflexagon and they also make an interesting hexaflexagon. The first few braids can be found here. Note that the video shows the 5-sided version, with the sides numbered from 1-5 instead of 0-4. Bronze HexaflexagonThis one is made from 30-60-90 (bronze) triangles. When the 60 degree angles are in the center, you have a flat triangle. When the 90 degree angles are in the center, it doesn’t lie flat, giving you sort of a flower shape. When the 30 degree angles are in the center, you get a cone that doesn’t open all the way so you can’t flex through to the next position. Cut out the net and pre-crease all the edges. Copy the small numbers on to the back. For the three sided version, fold adjacent 3’s together and tape the tabs onto the appropriate faces labeled with a 2. Doing a pinch flex on side 1 gives you a cone with 3 on the inside. Doing a pinch flex on a side 2 gives you side 3 as a tripod. A second pinch flex gives you a cone with side 1 on the inside.
With this six sided version, start by folding 6 on 6, 5 on 5 and 4 on 4. If you then fold 2 on 2, you can fold it into a cone shape with 1’s on the outside and 3’s on the inside, allowing you to tape the flaps onto the appropriate faces. From here, two successive pinch flexes give you a triangle with 3 on one side and 2 on the other. With experimentation, you should be able to find all 6 faces. This is the equivalent of a hexahexaflexagon made from a straight strip, so knowing the Tuckerman traverse for that one will help you figure out this one.
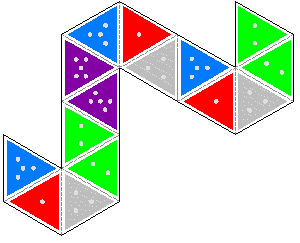
However, due to the right angles, there are additional flexes you can do. Start from the state where 2’s are on one side and 3’s are on the other. Fold it in half in any direction. You should be able to find a flap that opens up flat into a diamond shape with an extra triangle sticking off the edge. This flap can be folded backwards along the opposite diagonal. When you open up the resulting shape, you’ll have a cone with the faces mixed up. You can flex from here into a triangle. 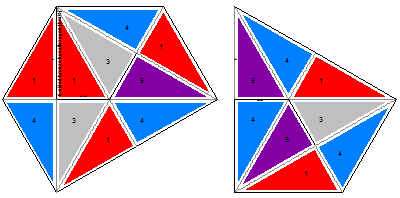Star HexaflexagonThis one is tricky to fold because of the sharp angles. It's also not quite as interesting as some of the other star flexagons, e.g. the star dodecaflexagon. 
Cut along the solid lines and pre-fold along the dashed lines. Copy the small numbers onto the backs of the triangles. Fold each pair of adjacent 3's together so you have a 3 pointed star. Tape the first and last triangles together, leaving you with all 1's on one side and all 2's on the other. One flex that works on this star flexagon is the pivot flex. Next: The Heptaflexagon |
