
|
There are many varieties of flexagons you can make from triangles. One method for designing one is to start from a hexaflexagon strip and vary the angles in the triangles and/or the number of copies of the underlying pattern. Another method is to start from a long strip and paste together all adjacent faces of a particular number. You can also use a sequence of flexes to generate a flexagon. See flexagon generating sequences for more information on this technique. Vary the angles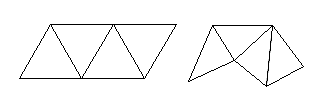
The hexaflexagon strip uses equilateral triangles but any triangle will do. As you traverse the states of a flexagon, the triangles rotate relative to each other so each angle can be combined with other instances of the same angle in the center. When you start from a triangle where each of the three angles is different, the states of the flexagon can look quite dissimilar. For example if you have six 30-60-90 triangles, sometimes youíll have 6x60=360 degrees filled allowing the flexagon to lie flat, sometimes youíll have 6x90>360 so it might have a flower-like appearance and sometimes youíll have 6x30<360 so you canít fully open it up. But you canít just connect any old triangles together any way you want. The first key is that all the triangles have to be congruent, i.e. they all have the same angles and lengths. The second key is that when you add a triangle to the strip, it has to be mirrored across the connecting edge. A general property thatís useful is to have every triangle connect to exactly two other triangles once theyíre folded together. You can have them connect to more, but youíll find that you canít reach some of the faces through flexing. An isosceles triangle, where two of the angles are the same, can be interesting because two of the three configurations are the same. A right triangle can be interesting because the 90 degree angle sometimes opens up new flexing options due to the ability to fold it at right angles along two of its sides. An equilateral triangle can be aesthetically pleasing because all three configurations are the same. A 45-45-90, or ďsilverĒ, triangle can be interesting both because it can lie flat in two of its three configurations and because it has a right angle. Vary the number of pattern copies
Another way to get variety is change the number of times you repeat the underlying pattern. If you look at an unfolded hexaflexagon, youíll see that it typically consists of the same pattern of numbers repeated three times. (If the number of faces is odd, the middle pattern will start on the opposite side of the strip.) If you repeat the pattern a different number of times, youíll get a different flexagon. The number of times you repeat the pattern determines how many triangles will meet in the center and has a big impact on the dynamic behavior. Repeat the hexaflexagon pattern four times instead of three and you have eight triangles meeting in the middle instead of six. So letís put this all together with a specific example. For a dodecaflexagon, you use 6 copies of a pattern instead of three and you use 30-60-90, or ďbronzeĒ, triangles instead of equilateral triangles. Knowing this allows you to derive a dodecaflexagon from a hexaflexagon strip. A dodecaflexagon is particularly rich in symmetry since 12 is divisible by 2, 3, 4 and 6, thus you can fold it in half, thirds, quarters or sixths. You can do a pinch flex with 3-fold symmetry that matches what you can do on a hexaflexagon. But you can also do a pinch flex with 6-fold symmetry. Youíll start with all 12 triangles having their 30 degree end pointing at the middle. This works nicely because that adds to 360. But as you flex, youíll pass through a stage where all the 60 degree angles point to the center and all 90 degree angles point at the center. These obviously wonít lie flat. Make shorter strips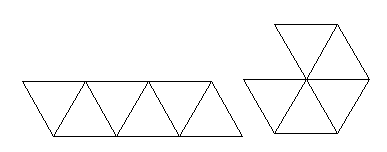
Another way to create new strips is to start from a long strip and paste together all adjacent pairs of a given number. For example, a straight strip of 18 equilateral triangles with the numbering 1/4, 2/4, 3/5, 1/5, 2/6, 3/6 leads to a 6-sided hexaflexagon (where 1/4 means the front side is labeled 1 and the back side of the same triangle is labeled 4 and the pattern is repeated three times). If you paste together each of the adjacent pairs of 6ís, youíll have the strip for a 5-sided hexaflexagon. Thereís a simple way to generate arbitrarily long hexaflexagon strips. The 3-sided version comes from a straight strip of 9 triangles labeled 1/2, 1/3, 2/3 repeated three times. To make the 6-sided version, double the number of triangles to get 18. Number the back 4, 4, 5, 5, 6, 6. Fold these adjacent numbers together to get a strip of 9 triangles. Label these with the 3-sided numbering, making sure that adjacent pairs of numbers span a break, i.e. if you unfolded the stip, there would be no adjacent 1ís, 2ís or 3ís. To make the 12-sided version, double the number of triangles again. Label the back 7, 7, 8, 8, 9, 9, 10, 10, 11, 11, 12, 12. Fold these together. Repeat the above steps to determine the new numbering. Once you have your long strip (though not too long, since it becomes unwieldy pretty quickly), you can create a flexagon of any number of sides less than what you have through the pasting technique. Then you can vary the angles in the triangle and/or the number of copies of the underlying pattern to generate arbitrary triangle flexagons. Thereís a lot of variety to explore. New flexings become possible with novel flexagons. Odd ordered flexagonsA trihexaflexagon has 3 sides and 6 triangles per face for a total of 18 numbered triangles. Since each leaf has two sides, this means the unfolded strip has 9 triangles. If, however, you wanted to make a tripentaflexagon, you would need 3 x 5 = 15 numbered triangles. This obviously isnít possible since you have to have an even number owing to the fact that every triangle has two sides. In general, youíll have more success in making an odd ordered flexagon if you start from a strip designed for an even number of sides. Note however, that you wonít be able to flex it in such a way that the faces will stay intact. Youíre also going to have different dynamic behavior with an odd ordered flexagon. The standard hexaflexagon-style pinch flex operates by swapping leaves between adjacent pats (stacks of triangles), hence the pats work in pairs called sectors. Since the pats in an odd ordered flexagon canít be divvied up in pairs, you canít get equivalent behavior. A typical technique is to flex a portion of it using a flex that works on a smaller ordered flexagon. For example, you can use a hexaflexagon pinch flex on a heptaflexagon, but a pair of triangles will end up not lying flat once youíre through. 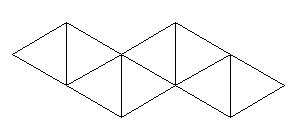
|
