|
The following collection of unique dice are all fair dice.
As far as I know, this is the first time many of these shapes have been turned into dice.
They're all available at my shop on Shapeways.
| sides | nick name | shape | type |
| 4 | double prism | gyrobifastigium | order 2 polyisohedron |
| 5 | jack | lat-long | order 3 polyisohedron |
| 6 | die-pyramid | triangle dipyramid | isohedron |
| 7 | cone | lat-long | order 3 polyisohedron |
| 8 | fusion | tetragonal trapezohedron | isohedron |
| 9 | barrel | lat-long | order 3 polyisohedron |
| 10 | gyro | lat-long | order 2 polyisohedron |
| 12 | die-pyramid | hexagonal dipyramid | isohedron |
| 12 | suspension | triakis tetrahedron | isohedron |
| 12 | caltrop | tetrahedron cumulation | isohedron |
| 12 | pyrite | octahedral pentagonal dodecahedron | isohedron |
| 12 | tetartoid | tetragonal pentagonal dodecahedron | isohedron |
| 30 | d30 | twice zonohedrified icosahedron | order 3 polyisohedron |
d4 - double prism
This 4 sided die is a gyrobifastigium, an order 2 polyisohedron.
It has 4 square sides and 4 equilateral triangle sides, though only the square sides are stable.
One nice thing about this shape is that it rolls better than the standard 4 sided die, the tetrahedron, since it has twice as many sides.
It's also a bit easier to read the result.
d5 - jack
This 5 sided die has a convex hull that's a lat-long polyisohedron, an order 3 polyisohedron.
It consists of an overall star shape with 5 sided pyramids on each side.
When rolled, it can land either just on the points of the star or on points of the star and the tip of one of the pyramids.
It's numbered in such a way that there are 5 possible outcomes, each appearing with equal probability.
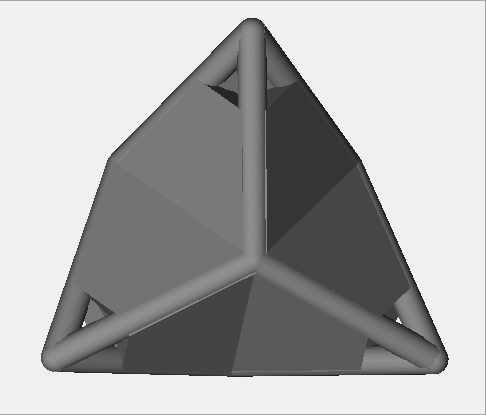
d6 - die-pyramid
This 6 sided die has a convex hull that's a triangle dipyramid, an isohedron.
Since a triangle dipyramid doesn't have parallel opposite sides, I started from a wireframe.
Then I created a shape inside it that has sides parallel to the outside shape.
The result is a novel 6 sided die.
d7 - cone
This 7 sided die is a lat-long polyisohedron, an order 3 polyisohedron.
Though this shape has 21 sides, only 7 of them are stable, each of which appear with equal probability.
The numbered sides are offset from the other sides so it's easy to read the result of a roll.
d8 - fusion
This 8 sided die has a convex hull that's a tetragonal trapezohedron, an isohedron.
I embedded two pyramids inside each other to make this die.
Its convex hull doesn't have parallel opposite sides, so this is a nice way to create an elegant 8 sided die out of this shape.
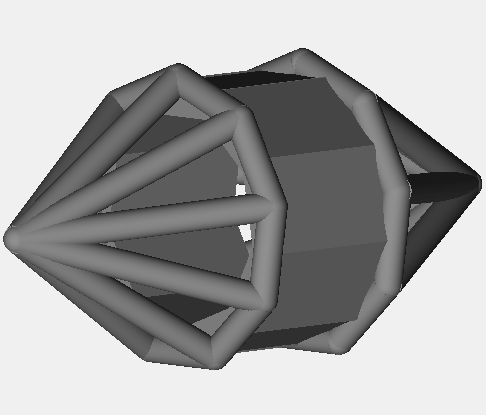
d9 - barrel
This 9 sided die is a lat-long polyisohedron, an order 3 polyisohedron.
Though this shape has 27 sides, only 9 of them are stable, each of which appear with equal probability.
The numbered sides are offset from the other sides so it's easy to read the result of a roll.
d10 - gyro
This 10 sided die is a lat-long polyisohedron, an order 2 polyisohedron.
There are actually 20 triangular sides to this shape, where the sides aren't all equivalent.
I've combined adjacent pairs together so that each of the resulting 10 sides can be rolled with equal probability.
d12 - die-pyramid
This 12 sided die is a hexagonal dipyramid, an isohedron.
This shape works very nicely as a die, providing an elegant alternative to the regular dodecahedron.
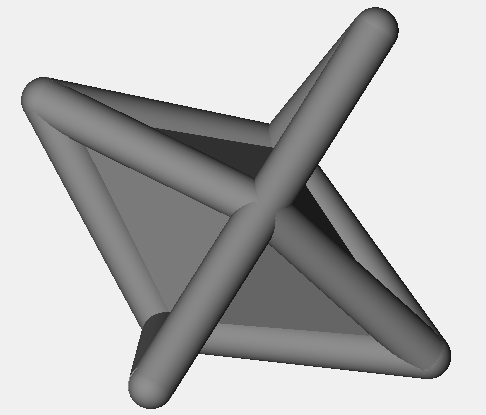
d12 - suspension
This 12 sided die has a convex hull that's a triakis tetrahedron, an isohedron.
The triakis tetrahedron is a tricky shape to turn into a die since opposite sides aren't parallel.
But by embedding a second triakis tetrahedron inside a wireframe, I was able to create parallel sides.
The end result is a very distinctive 12 sided die.
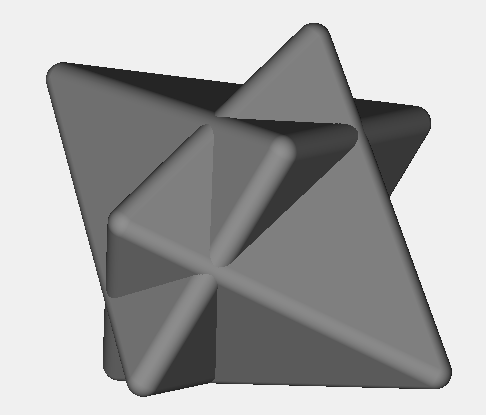
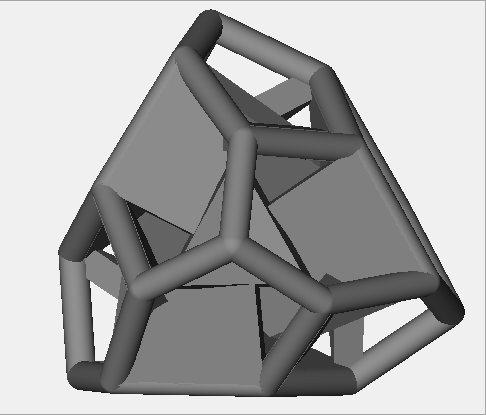
d12 - caltrop
This 12 sided die is a tetrahedron cumulation, an isohedron.
Like the suspension, it has a convex hull that's a triakis tetrahedron.
The result is read off of the side that's parallel to the table, rather than the side that's on top.
d12 - pyrite
These 12 sided dice are octahedral pentagonal dodecahedra, an isohedron.
It's also known as a pyritohedron, since it's one of the crystal forms of pyrite.
I've chosen just a couple of the infinite variety of pyritohedra.
They typically look like a slightly warped version of a regular dodecahedron or rhombic dodecahedron.
d12 - tetartoid
This 12 sided die is a tetragonal pentagonal dodecahedron, an isohedron.
Crystallographers know it as the tetartoid.
It's a challenging shape to turn into a die since opposite faces aren't even close to being parallel.
To make it work, I started from a wireframe of the shape then embedded parallel sides inside it.
The result is one of the most unlikely looking dice I've seen.
d30
This 30 sided die is a twice zonohedrified icosahedron, an order 3 polyisohedron.
Though it actually has 90 sides, this design behaves much like a rhombic triacontahedron.
Fair dice
|