
Polyhedral transformsThere are many ways to morph between various of the isohedra with polyhedral symmetry. One elegant set of transforms I call the isohedral triangle, quadrilateral and pentagonal transforms. These transforms start from one of the three basic polyhedral symmetry classes Ė tetrahedral, octahedral or icosahedral Ė to produce a continuum of isohedra. Iíll refer to these symmetry classes as T or 4, O or 8, and I or 20 respectively. Each symmetry group has an associated base polyhedron with equilateral faces: the tetrahedron, octahedron and icosahedron. There are three sets of axes in each symmetry group that are important to these transforms, corresponding to the vertices, faces and edge midpoints of the base polyhedron. 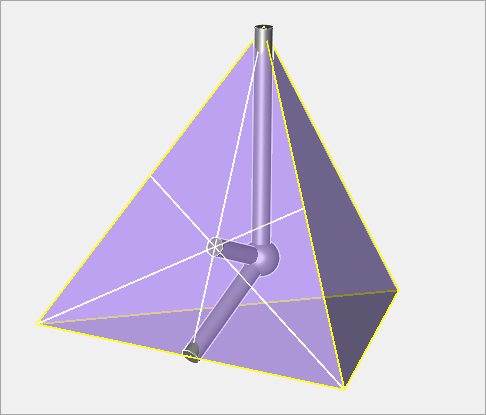


Note that with each of these transforms, itís assumed that adjacent faces are merged into one if theyíre co-planar. For an explanation of the isohedral notation, see the isohedra page. Isohedral triangular transformEach of the sets of points (vertex, face and edge) can be raised and lowered independently while maintaining the polyhedronís isohedral properties. You can keep one set of points fixed while varying the other two sets without any loss of generality, thus this transform has two degrees of freedom and produces an infinite number of isohedra. Iíll use the notation #t(f, e) to describe an isohedral triangle transform, where # is the symmetry class, f is the distance from the center of the polyhedron to the points on the face axis and e is the distance from the center of the polyhedron to the points on the edge axis. The distance from the center to the points on the vertex axis is assumed to be 1. In the most general case, each equilateral triangular face from the base polyhedron gets broken into 6 congruent scalene triangles. Hence the number of maximum number of faces for each symmetry class is 24, 48 and 120. Adjacent faces can be combined when they are co-planar, so there may be fewer faces as well. For T, there may be 4, 6, 12 or 24 faces. For O, there may be 6, 8, 12, 24 or 48. For I, there may be 12, 20, 30, 60 or 120. T has fewer possibilities because the vertex and face axes are equivalent, i.e. the tetrahedron is its own dual. 4tThe graph below shows the various isohedra that can be made using the tetrahedral triangular transform, 4t. It lists different lengths for the face and edge axes and charts the values used to generate different classes of isohedra using the isohedral notation described on the isohedra page. The dark text represents a specific shape while light text represents an infinite collection of shapes, e.g. the dark 12T is the triakis tetrahedron Catalan solid, while the light 12T labels the line representing the infinite class of triakis tetrahedra. 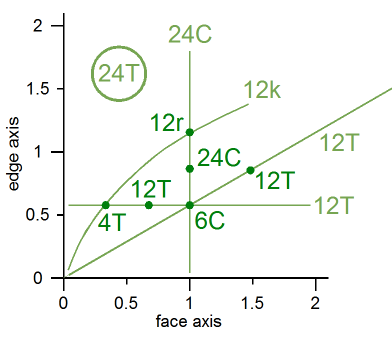
The following series uses the tetrahedral symmetry group. It just changes the face axis, ranging from 4t(0.167, 0.577) to 4t(1.67, 0.577). It includes the tetrahedron, triakis tetrahedron, cube and triakis tetrahedron made from equilateral triangles. 









The following series uses the tetrahedral symmetry group. It just changes the edge axis, ranging from 4t(1, 0.4325) to 4t(1, 1.3). It includes the cube, tetrakis hexahedron and rhombic dodecahedron. 






8tThe graph below shows the various isohedra that can be made using the octahedral triangular transform, 8t. It lists different lengths for the face and edge axes and charts the values used to generate different classes of isohedra using the isohedral notation described on the isohedra page. The dark text represents a specific shape while light text represents an infinite collection of shapes, e.g. the dark 24C is the tetrakis hexahedron Catalan solid, while the light 24C labels the line representing the infinite class of tetrakis hexahedra. 
The following series uses the octahedral symmetry group. It just changes the face axis, ranging from 8t(0.437, 0.707) to 8t(1.0105, 0.707). It includes the octahedron and rhombic dodecahedron. 




The following series uses the octahedral symmetry group. It changes both the face and edge axes, ranging from 8t(0.577, 0.707) to 8t(1.732, 1.414). It includes the octahedron and cube. 




The following series uses the octahedral symmetry group. It changes both the face and edge axes, ranging from 8t(0.8255, 0.5605) to 8t(0.9875, 1.1465). It includes the rhombic dodecahedron, hexakis octahedron and trapezoidal icositetrahedron. 




20tThe graph below shows the various isohedra that can be made using the icosahedral triangular transform, 20t. It lists different lengths for the face and edge axes and charts the values used to generate different classes of isohedra using the isohedral notation described on the isohedra page. The dark text represents a specific shape while light text represents an infinite collection of shapes, e.g. the dark 60D is the pentakis dodecahedron Catalan solid, while the light 60D labels the line representing the infinite class of pentakis dodecahedra. 
The following series uses the icosahedral symmetry group. It changes just the face axis, ranging from 20t(0.735, 0.851) to 20t(0.969, 0.851). It includes the icosahedron and rhombic hexacontahedron. 




The following series uses the icosahedral symmetry group. It changes both the face and edge axes, ranging from 20t(0.911, 0.851) to 20t(1.258, 1.176). It includes the rhombic hexacontahedron and dodecahedron. 



Isohedral quadrilateral transformThis transform modifies quadrilateral faces. One face corner is along the vertex axis with the opposite corner along the face axis. The other two corners are along edges of the base polyhedron. One way to perform this transformation is to pivot across the diagonal connecting the edge corners, raising and lowering the vertex and face axes points. In the most general form of this transform, the two edge corners can be anywhere along the edge of the base polyhedron (rotational symmetry giving you the second point once youíve chosen the first). Due to parity, however, only octahedral symmetry permits points other than the edge midpoints. With tetrahedral and icosahedral symmetry, the edge points must be on the edge axes (and hence at the midpoints of the edges). In these cases, this transform just becomes a special case of the isohedral triangular transform. Iíll use the notation #q(v, e1) to describe the isohedral quadrilateral transform, where # is the symmetry class, v is the distance from the center of the polyhedron to the points on the vertex axis and e1 is the fractional distance along the edge where the pivot points are. From these values, f (the distance from the center to the points on the face axes) can be determined. Note that e1 must be 0.5 for tetrahedral and icosahedral symmetry. When e1 is 0.5, the faces are kites, where adjacent pairs of edges are equal. For other values of e1, the two edges originating from the face vertex are the same length. The other two sides are different lengths in the general case. 4qThe following series uses the tetrahedral symmetry group. It changes just the vertex axis, ranging from 4q(0.29167, 0.5) to 4q(0.5, 0.5). It includes the tetrahedron, rhombic dodecahedron and various trapezoidal dodecahedra. 





8qThe graph below shows the various isohedra that can be made using the octahedral quadrilateral transform, 8q. It lists the fractional distance along an edge versus the length of the vertex axis and charts the values used to generate different classes of isohedra using the isohedral notation described on the isohedra page. The dark text represents a specific shape while light text represents an infinite collection of shapes, e.g. the dark 24k is the trapezoidal icositetrahedron Catalan solid, while the light 24k labels the line representing the infinite class of trapezoidal icositetrahedra. 
The following series uses the octahedral symmetry group. It changes just the vertex axis, ranging from 8q(0.375, 0.5) to 8q(1.125, 0.5). It includes the cube, trapezoidal icositetrahedron and octahedron. 






The following series uses the octahedral symmetry group. It changes both the vertex axis and the distance along the edge axis, ranging from 8q(0.375, 0.625) to 8q(0.999, 0.001). It includes the cube and various pyritohedra. It approaches the rhombic dodecahedron as x approaches 1 in 8q(x, 1-x), but 8q(1, 0) is an octahedron. 





20qThe following series uses the icosahedral symmetry group. It changes just the vertex axis, ranging from 20q(0.5, 0.5) to 20q(1.125, 0.5). It includes the rhombic hexacontahedron, dodecahedron and icosahedron. 





Isohedral pentagonal transformThis transform modifies pentagonal faces. One corner is along the vertex axis with a second, non-adjacent corner along the face axis. The other three corners are offset from the edges of the base polyhedron. Iíll use the notation #p(e1, e2) to describe the isohedral pentagonal transform, where # is the symmetry class and e1 and e2 are used to describe the location of the three corners that are derived from the base polyhedronís edges. e1 is a fraction of the distance along the edge, while e2 is the perpendicular distance from the plane made by the edge and the center of the polyhedron. Two other points are then symmetrically chosen. Take the plane containing those three points and find the intersection of that plane with the vertex and face axes to determine the final two points of the pentagonal face. The two edges originating from the point on the vertex axis are equal length as are the two edges originating from the point on the face axis. The fifth edge can be unequal to the other four. This means there are three different ways for the pentagonal faces to have bilateral symmetry:
4pThe graph below shows the various isohedra that can be made using the tetrahedral pentagonal transform, 4p. It lists the distance from the edge plane versus the fractional distance along an edge and charts the values used to generate different classes of isohedra using the isohedral notation described on the isohedra page. 
The following series uses the tetrahedral symmetry group. It ranges from 4p(0.21585, 0) to 4p(0.5, 0.23435). It includes the tetrahedron and dodecahedron. 






The following series uses the tetrahedral symmetry group. It ranges from 4p(0.5, 0.18) to 4p(0.3217, 0.52635). It includes the tetrahedron and cube. 





8pThe graph below shows the various isohedra that can be made using the octahedral pentagonal transform, 8p. It lists the distance from the edge plane versus the fractional distance along an edge and charts the values used to generate different classes of isohedra using the isohedral notation described on the isohedra page. 
The following series uses the octahedral symmetry group. It ranges from 8p(0.2955, 0.3999) to 8p(0.5409, 0.0192). It includes the rhombic dodecahedron and cube. 






The following series uses the octahedral symmetry group. It ranges from 8p(0.4088, 0) to 8p(0.4479, 0.4479). It includes the octahedron, pentagonal icositetrahedron and rhombic dodecahedron. The fifth shape in the series is an interesting one I haven't seen mentioned elsewhere. Like the pentagonal icositetrahedron, its faces have bilateral symmetry. 







20pThe graph below shows the various isohedra that can be made using the icosahedral pentagonal transform, 20p. It lists the distance from the edge plane versus the fractional distance along an edge and charts the values used to generate different classes of isohedra using the isohedral notation described on the isohedra page. 
The following series uses the icosahedral symmetry group. It ranges from 20p(0.1385, 0.0886) to 20p(0.5, 0.0886). It includes the rhombic dodecahedron, pentagonal hexecontahedron and dodecahedron. 





The following series uses the icosahedral symmetry group. It ranges from 20p(0.2271, -0.0626) to 20p(0.465, 0.2505). It includes the icosahedron. The last shape in the series is an interesting one I haven't seen mentioned elsewhere. Like the pentagonal hexecontahedron, its faces have bilateral symmetry. 





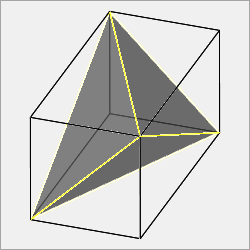
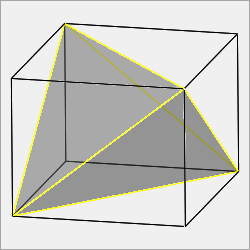
Disphenoid transformThis transform embeds a tetrahedron in a cuboid with edges of length 1, a and b. I'll use the notation 4d(a, b) to describe this transform. If a=b, the faces are isosceles triangles and the shape is a tetragonal disphenoid. In the general case, the faces are scalene triangles and the shape is a rhombic disphenoid. 

|
