
|
A polyhedron is a polyisohedron if its faces can be grouped into sets that are equivalent. Definitions:
As an example, consider a Johnson solid with an entertaining name, the gyrobifastigium. It has 4 equilateral triangle faces and 4 square faces. You can pair up each triangle with a square so you have 4 polyfaces. Hereís one way to arrange them into congruent polyfaces, creating an order 2 polyisohedron with 4 polyfaces: 
Here's a second way to create congruent polyfaces: 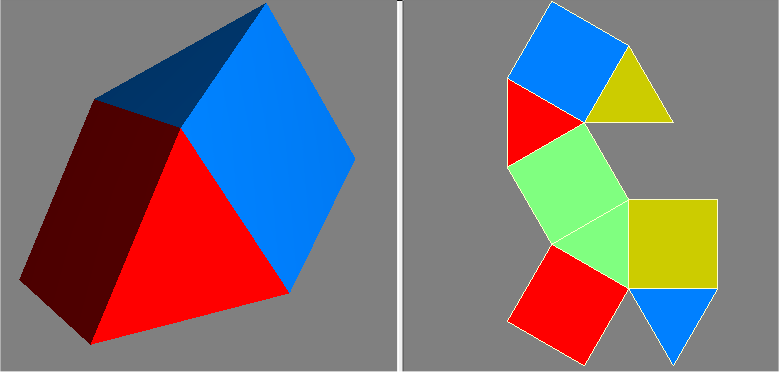
With this next way of pairing up the triangles and squares, the 4 polysides arenít congruent, hence it isn't polyisohedral: 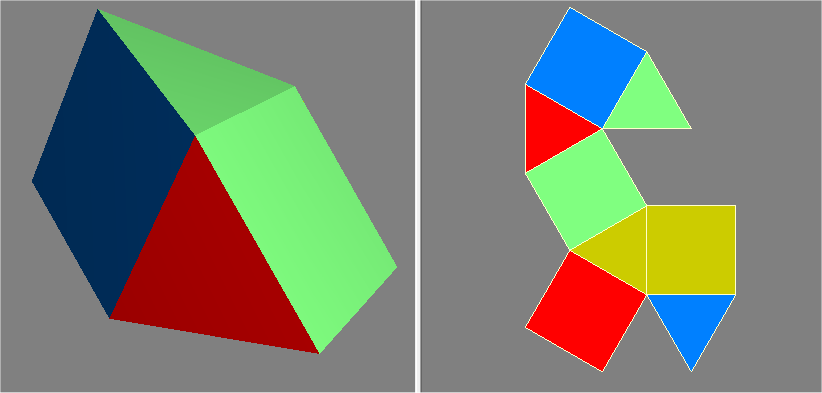
Lat-long polyisohedronA lat-long polyisohedron uses a generalization of latitude and longitude on a sphere. To make one, start with a series of connected line segments. Create multiple equally spaced copies around the axis that connects the start and end point of the segments. The following example shows an order 4 lat-long polyishedron with 5 polyfaces. 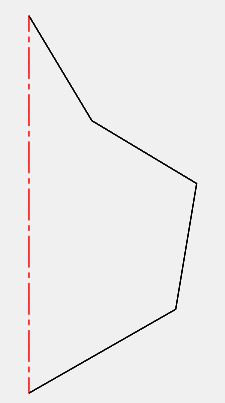
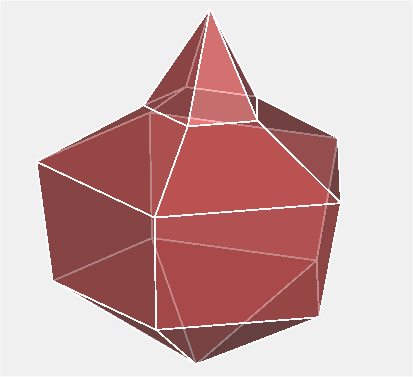
If there are m line segments and n copies, the result will be an order m polyisohedron with n polysides. Each polyside will consist of two isosceles triangles and m-2 trapezoids. The lat-long polyisohedron construction demonstrates that polyisohedra of any order 2 and greater exists with any number of sides 3 and greater. In contrast, order 1 polyisohedra, the isohedra, can't have an odd number of sides. They can have any number of even sides 4 and greater. Other examples





|
