
|
Square tetraflexagons are an interesting type of flexagon because they're simple to make, simple to flex and yet have all the intriguing complexity of other flexagons. They're folded from linked squares into a set of four squares that make up a bigger square. I start by showing a 7-sided flexagon that supports a good variety of flexes and cycles. Then I provide a collection of square tetraflexagons based on the flexes used to create them, a different presentation than you generally see. To make the 7-sided square tetraflexagon:
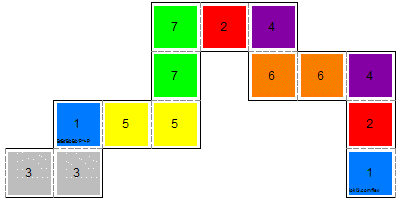
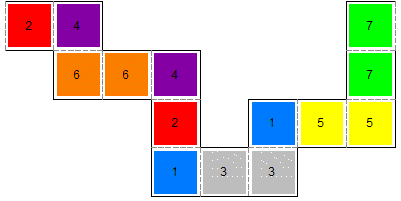
Square tetraflexagonsTo understand the remainder of this page, it's useful to understand some terminology and notation. I'll use 1/2 to indicate a state where the top side consists of all 1's and the bottom side of all 2's. A flex is a way to manipulate the flexagon that takes you from one state to another. Flex notation is a short-hand for describing a series of flexes, A generating sequence is a way to describe the construction of a particular flexagon from a sequence of flexes. General instructions for how to create a flexagon from the templates:
Pinch flex
The most basic flex is the pinch flex. On a square tetraflexagon, you simply fold it in half and unfold it from the opposite side. It's directly analogous to the pinch flex on triangle flexagons. In flex notation, the pinch flex is represented as P. The following is the simplest flexagon to allow the pinch flex: 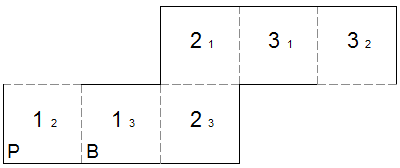
template for square tetraflexagon with generating sequence P Once you've performed a pinch flex on a square tetraflexagon, there are four places you could do a second pinch flex. One option is to flip the flexagon over and do a second pinch flex along the same axis. In flex notation, this action is represented as ^P. This is equivalent to performing the pinch flex in reverse, represented as P'. This will bring you back to your original state. This can be represented as I = P^P = PP'. A second option is to perform a second pinch flex in the same place, represented as PP (ie. a pinch flex followed by a pinch flex in the same place). The following flexagons are the simplest ones that support PP, PPP and PPPP: 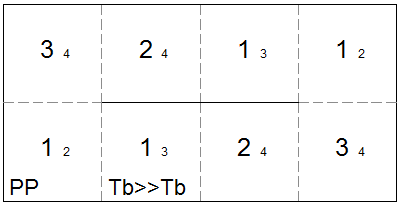
template for square tetraflexagon with generating sequence PP 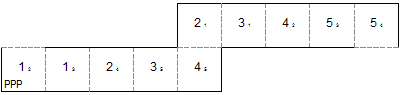
template for square tetraflexagon with generating sequence PPP 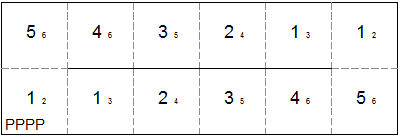
template for square tetraflexagon with generating sequence PPPP A third option is to rotate the flexagon 90 degrees and do a pinch flex there. This is represented as P>P (i.e. pinch flex, rotate once to the right, pinch flex). Once the flexagon supports P>P, you can step through a cycle of four states where you rotate the flexagon before each subsequent pinch flex. In flex notation, this is expressed as I = P>P>P>P>. Here's what that flexagon looks like: 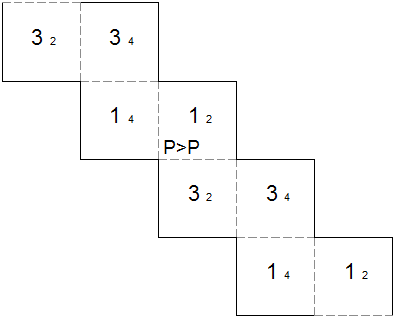
template for square tetraflexagon with generating sequence P>P It's interesting to note that there's another way to do P>P. If you try the next flexagon and pay close attention to the pinch flexes you do, you can see that there are two subtly different types of flexes. One takes leaves from the pat on the left, while the other takes leaves from the right. This is described by the flex sequence Pl>Pr. On the following flexagon, I = Pl>Pl>Pr>Pr>. 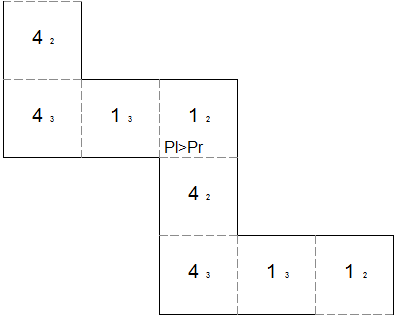
template for square tetraflexagon with generating sequence Pl>Pr The fourth option is to turn the flexagon over, rotate one step and perform a pinch flex there. This is represented as P^>P. Doing this n times is represented as (P^>)xn. The following flexagons use various values of n for their generating sequences. 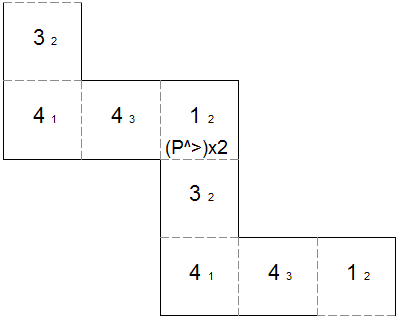
template for square tetraflexagon with generating sequence (P^>)x2 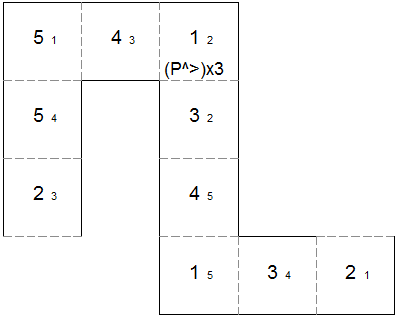
template for square tetraflexagon with generating sequence (P^>)x3 
template for square tetraflexagon with generating sequence (P^>)x4 Box flexWhen you try the flexagon with a generating sequence of P, you'll see that you can flex between states 1/2 and 2/3, where both states seem like dead ends. But you'll find that, from both sides 1 and 3, you can open the flexagon into a box. This is called the box flex, represented as B in flex notation. If you look at the box flex you can do from side 1, you'll see 3 on the inside. If you look at the box flex you can do from side 3, you'll see 1 on the inside. In other words, if you could turn the box inside out, you'd be able to cycle between states 1/2, 2/3 and 3/1 without any dead ends. While this may seem uninteresting on a square tetraflexagon, it becomes much more interesting when you replace the square with a different quadrilateral, one that allows you to essentially turn the box inside out like a trapezoid. Considering the boxed state to be an independent state is especially useful when comparing flexagons made from different quadrilaterals. (One interesting option is to treat the boxed state as a flexatube in order to turn it inside out, completing the cycle.) 
template for square tetraflexagon with generating sequence B On a square tetraflexagon, the box flex becomes more interesting when you can open the box back up a different way. Just before you open the box, two of the hinges are flat. If you continue to flex through the box position, you can make the other two hinges flat. From here, you may be able to open the box back up from either the top or the bottom, sometimes both. If you open the box back up from the top, it's Bt. If you open it from the bottom, it's Bb. The first flexagon below has Bt as it's generating sequence while the second one uses Bb. 

template for square tetraflexagon with generating sequence Bt 
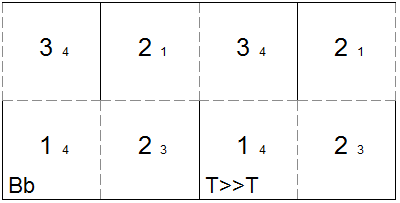
template for square tetraflexagon with generating sequence Bb (or T>>T) An alternate way to view Bt and Bb is to consider them to be a sequence of flexes starting with B. Then Bt=B>P and Bb=B>P'. This can make drawing a state diagram easier and makes the correspondence between related quadrilateral flexagons more obvious. Tuck flex
The tuck flex is tricky to perform on a square tetraflexagon. It's easier on some triangle flexagons (see tuck flex) or flexagons made of other quadrilaterals, such as kites or trapezoids. I'll introduce it here because it's interesting to note the variations. If you try it, I recommend using a flexagon you don't mind bending and possibly taking apart and reconnecting if you get lost. See the video for a demonstration of tuck flexes. One unique aspect of the tuck flex is that it has requirements beyond just the pats involved directly in the flex. It requires that you be able to open up other parts of the flexagon in order to allow enough degrees of freedom to do the flex (but perhaps you could get around that if you made your flexagon out of rubber). Though this next flexagon has a generating sequence of T>>T (tuck flex, rotate two vertices, do another tuck flex), the second tuck flex is extremely difficult to do without ripping the flexagon. An easier approach, though still difficult, is to instead do an inverse tuck from the opposite side, since T = ^T'^. 
template for square tetraflexagon with generating sequence T>>T 
This following flexagon demonstrates that you can do a tuck flex from the box state, represented as Tb. 
template for square tetraflexagon with generating sequence Tb The generating sequences PP and Tb>>Tb create the same flexagon. 
template for square tetraflexagon with generating sequence Tb>>Tb This flexagon has a generating sequence of T, but without an extra hinge on the opposite side it's almost impossible to flex. I've included it simply to show the theoretical minimum requirement for a tuck flex. 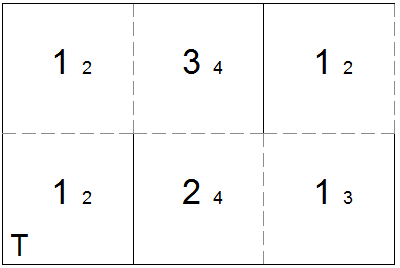
template for square tetraflexagon with generating sequence T Other generating sequencesFor this next flexagon, I chose a flex sequence that would allow me to do a box flex that could open from the top or bottom from either side of the initial position. I chose the flex sequence (BtBt'BbBb'^>)x2. Basically you do a flex then undo it to bring you back to the original state, then you do a different flex. 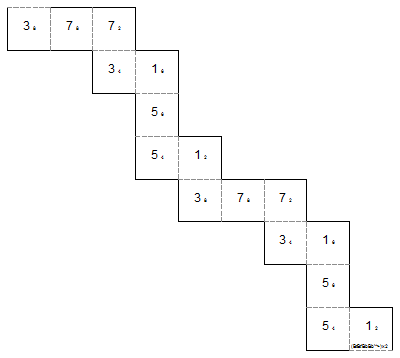
template for square tetraflexagon with generating sequence (BtBt'BbBb'^>)x2 For this last flexagon, I chose a flex sequence that would allow me to do a pinch (P), box top (Bt) or box bottom (Bb) from any position from state 1/2. This gave me a flex sequence of (PP'BtBt'BbBb'>)x2. 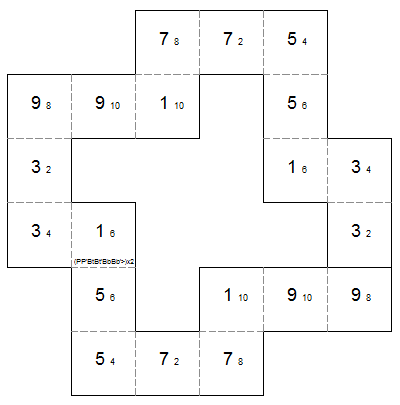
template for square tetraflexagon with generating sequence (PP'BtBt'BbBb'>)x2 |
