The pentaflexagon has 5 triangles meeting in the center.

• 8 sided version
• pyramid shuffle variants

At first glance, you may expect the pentaflexagon to be fairly uninteresting compared to other flexagons, given that it only has 5-fold symmetry. But there’s actually a surprising range of things you can do with this flexagon, from the simple pocket flex available on all variants to the slot flex and pyramid shuffle on some of the variants with more sides.

Using a series of slot flexes and pyramid shuffles, you can switch from having all 1’s on one side and 2’s on the other to having all 3’s on one side and 4’s on the other. It’s a challenging puzzle to figure out how to do this traversal. The video above shows how to operate this flexagon.

Click on the following thumbnail to get a large version. Print it and cut it out. Copy the small numbers on to the back. Start by folding 8a onto 4a and 5a onto 3a. Next fold 8b on 4b, 5b on 3b and 7b on 6b. Continue doing the same with c, d and e - 8 on 4, 5 on 3 and 7 on 6. It should end up turning into a pentagon. Finish by tucking the final flaps under each other so 7a and 6a are face to face with all 1’s on one side and all 2’s on the other. Tape together the edges of the first and last leaves in the strip to complete the flexagon.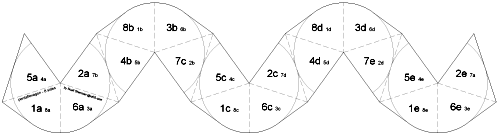

Alternately, you can use the following template instead. Click on each of the two thumbnails to get the larger version. Either print one on the back of the other, or print them on separate pieces of paper, cut them out and paste them back-to-back. On one end of the strip, 4 and 5 should be back-to-back. On the other end, 2 and 7 should be back-to-back. Where you find 8 and 4 next to each other, fold them together. Likewise with adjacent 5 and 3 combinations and 7 and 6 combinations. The video shows how this is done. Tape together the edges of the first and last leaves in the strip to complete the flexagon.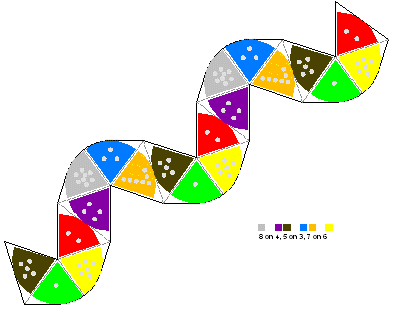

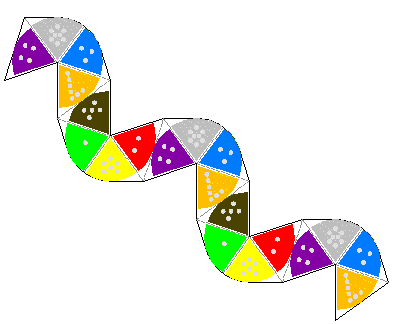
To do a slot flex from this initial arrangement, start by folding together two adjacent 2’s. This should allow you to do a pocket flex from side 1. The inside of the pocket will have 6’s and 7’s. A second pocket flex will reveal 3’s and 5’s. A third pocket flex will reveal 4’s and 8’s. You should now be able to slide one of the 8’s through the slot between the 2 and 4, turning the pyramid into a tetrahedron and the tetrahedron into a pyramid. The smooth curve along the 8 allows the slot flex to work without requiring you to bend the leaves. You can now perform the pocket flex three times on the pyramid to arrive back at a pentagon. If you pay attention to how you finished this series of flexes, you should be able to reverse the moves to come back to the original position.

To do a pyramid shuffle from the initial arrangement, fold together any pair of 2’s, then do a pocket flex from side 1. The inside of this pocket will have 6’s and 7’s. Now do a second pocket flex, but rather than opening it from the outside to reveal 3’s and 5’s, open it from the inside to reveal 3, 5, 6 and 7. This next step requires bending the leaves. The 1-3 pat and 1-5 pat need to bend so you can stuff them into the tetrahedron, with the top tip being shoved all the way down into the bottom tip of the tetrahedron. You will find that this arrangement opens back up into a pentagon. Folding together the 8 and 4 and repeating these steps will take you back to the original position.

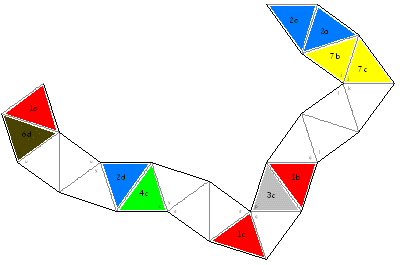
A combination of a single slot flex and a pair of pyramid shuffles changes a single leaf on each side. Done in the proper sequence, this can take you from the original arrangement of 1’s and 2’s to one with 3’s on one side and 4’s on the other. It’s a good challenge to figure out how to do this

I created the following two variants specifically so you could perform 5 pyramid shuffles in a row, but I chose a different flex sequence for each. The first was creating from the generating sequence S<<S<<S<<S<<S, while the second from the sequence S^S^S^S^S. (Note: An earlier version of this page incorrectly stated that the first generating sequence was S>>S>>S>>S>>S. Corrected 4-2012.) It's interesting how different their characters are. One has several cycles where you can repeat a series of pyramid shuffles, while the other only has dead ends in its state diagram. One allows you to go from a state with all 1's and 2's to a state with all 3's and 4's, while the other one always has the same four leaves visible even as everything else changes.

To create this first one, click on the following two thumbnails to get larger versions. Either print them out back-to-back, or cut them out and paste them back to back. The end of one sub-strip should have y on one side and z on the back, while the other end should have o on one side and p on the back. The end of the other sub-strip should have 2c on one side, with 1d on the back, while the other end has w on one side and v on the back. Tape together the two edges marked with * (labeled w and z) to make a single strip. Pre-crease all the edges. Now fold k on k, l on l, m on m, and so on, finishing with z on z. Tape together the edges of the first and last triangles.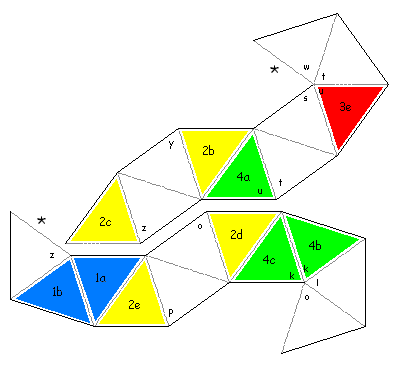

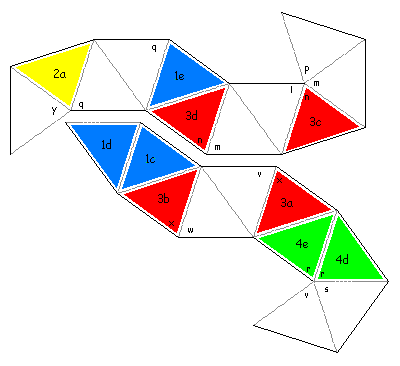
To create the next one, click on the following two thumbnails to get larger versions. Either print them out back-to-back, or cut them out and paste them back to back. Pre-crease all the edges. Now fold j on j, k on k, l on l, and so on, finishing with z on z. Tape together the edges of the first and last triangles.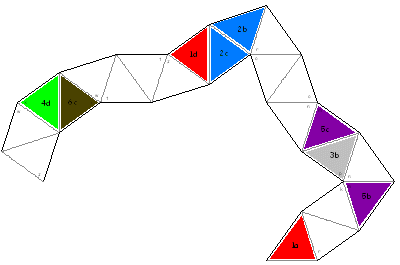

The following diagrams show all the states you can reach using the pyramid shuffle for the first variant above. Each pair of 5 numbers describes a single state, with each set of 5 describing one side. The order of the numbers matches the order of a, b, c, d, e, thus 32112 means that one side has 3a 2b 1c 1d 2e. A line between two numbers reflects where you can perform a pyramid shuffle. So, for example, if a line comes from between the first and second numbers, that means you start the pyramid shuffle by pinching together the back of leaves a and b with the given side facing toward you. The diagram on the right is an abstract representation of the overall graph.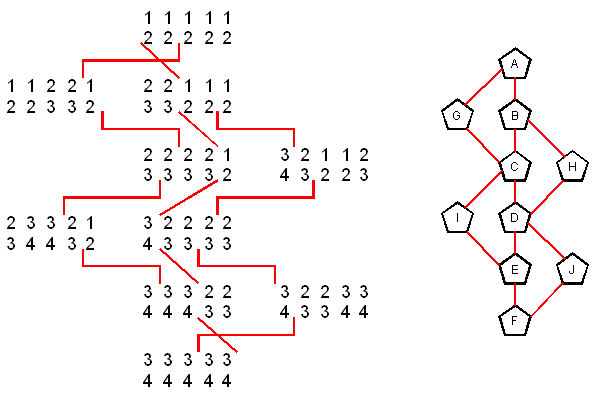

The next diagrams show all the states on the second variant above. It's interesting to note that the previous diagram has several cycles while this diagram has none. (Note: an earlier version of this page was missing states N, O, and P. Corrected 4-2012.)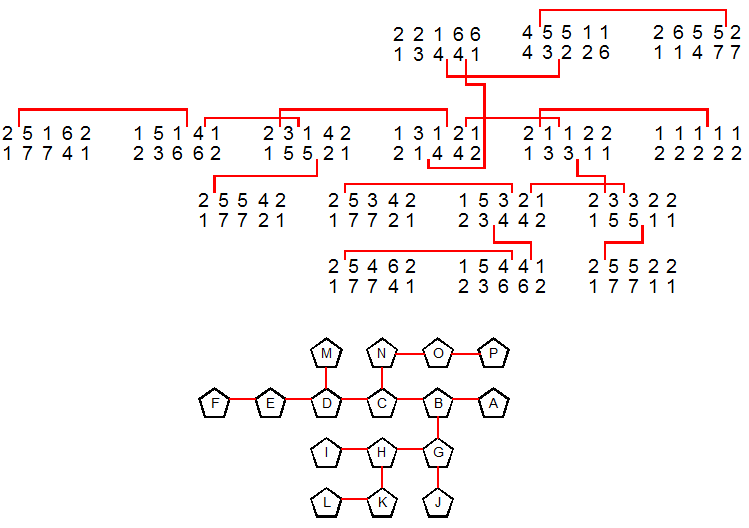

Next: The Hexaflexagon

Some of the possible flexes

Return to the Triangle Flexagon Bestiary