Multiple Numberings for Flexagons
|
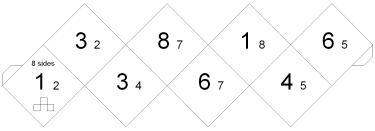
It’s possible to fold the same strip in different ways to create flexagons that behave differently. Square FlexagonThe first example is for 8-sided tetraflexagons. Click on the following strip to get a larger version and print two copies of it. Connect the two strips together to make a zigzagging strip of 16 squares. Crease all the edges before making the flexagon. Fold each 8 on the adjacent 8. Continue with 3 on 3, 2 on 2, 1 on 1, 7 on 7 and 4 on 4. You should end up with all the 5’s on one side and the 6’s on the other. Connect the two squares with the remaining flaps.
Do the same with the second strip, but fold in the following order: 7, 3, 5, 2 and 8. Then fold the adjacent 4’s together and tuck one end of the strip under the other so the 4’s are against each other. This should leave the 1’s and 6’s on the outside and make it easy to connect the flaps together.
When exploring these flexagons, you’ll need to use two different types of flexes to be able to reach all the sides. One method is to simply fold the flexagon in half and unfold it from the other side. The other is the “box flex”. You can try this out on the second flexagon by starting from face 6 when the 1’s are on the other side. Fold it in half either direction, leaving the 6’s on the outside. You should be able to open the center of the flexagon, with hinges on the top and bottom as well as left and right, leaving you with an open box. If you continue folding it till it’s lying flat again, you should be able to simply unfold it to see either side 5 or 7, depending on which way you folded it originally. 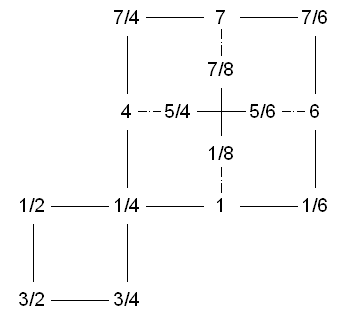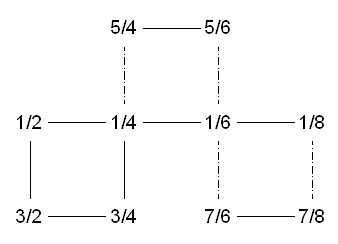The following graphs illustrate the different behavior of these two flexagons. 1/2 means that one side has all 1’s and the other has all 2’s. Solid lines represent a simple fold flex to get between two states. The box flex is represented by a dashed line. Sometimes when you fold it in half, you may be able to use either a simple flex or box flex to get to another state. I represent this middle state by only showing a single number in the graph with simple flexes and box flexes leading from it. 
Here's a list of alternate numberings for the above strip:
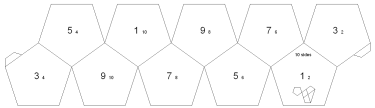
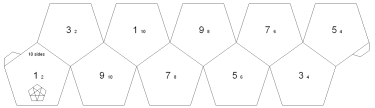
Pentagon FlexagonHere’s another example using a 10-sided pentagon flexagon. Proceed in the same way as with the tetraflexagons. Connect two copies of the strip and pre-crease the edges. Start by folding all the even numbers together – 2 on 2, 4 on 4, 6 on 6, 8 on 8 and 10 on 10. Then fold 9 on 9, 7 on 7 and 5 on 5. This’ll leave you with a strip with 1’s on one side and the 3’s on the other. Fold it in half, leaving only 1’s on the outside, and connect the flaps.
Pentagon flexagons are similar to tetraflexagons but have a few differences. The most notable is that it doesn’t lie flat in the main position, which looks a bit like a butterfly. The basic flex still works the same, however. Fold it in half then unfold it from the other side. You can also do a box flex from some positions. One additional move is the “snap flex.” When you’re in the main position with alternate pentagons tilting up and down, you can push down on the center to snap it through so the pentagons swap how they’re tilted. This allows you to fold the flexagon in half the other direction. This is only needed in the second flexagon to switch between the two cycles reachable from 1/5. Here are the state diagrams for the two flexagons above. 
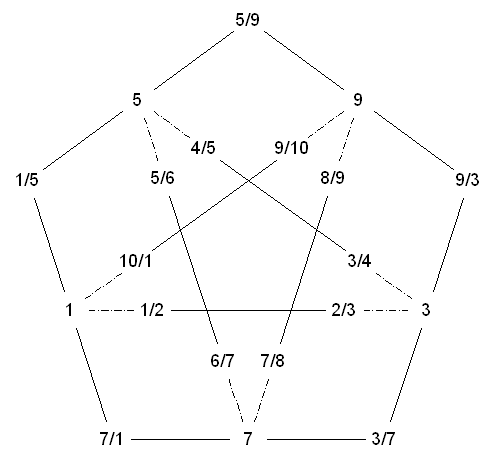
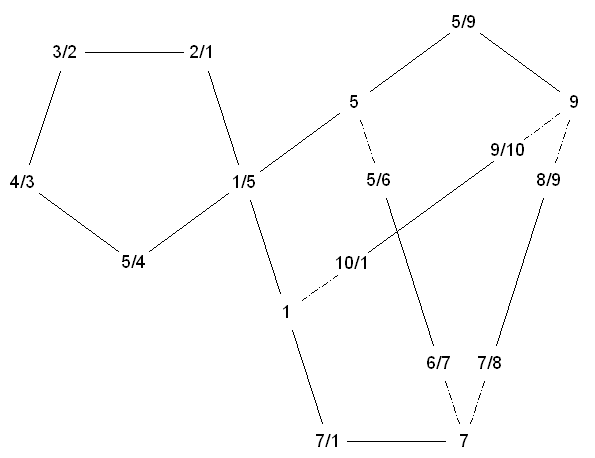
Here's a list of alternate numberings for the above strip:
HexaflexagonThe same thing is possible with hexaflexagons as well. If you start from a straight strip of equilateral triangles, the standard numbering is 4/7, 1/7, 2/8, 4/8, 5/9, 3/9, 1/10, 5/10, 6/11, 2/11, 3/12, 6/12. Trying 1/2, 1/12, 5/6, 5/4, 7/8, 7/6, 3/4, 10/9, 8/9, 3/2, 11/12, 11/10 instead leads to a different traversal of the faces. |
