The first chapter introduced flexagons and the pinch flex, describing how to use the Tuckerman Traverse to explore every face. The second chapter showed a variety of flexes and flexagons, demonstrating that there isn’t always a concept of well-defined “faces” on a flexagon.

This chapter will show how you can use generating sequences to custom design flexagons. A generating sequence is a sequence of flexes used to create the internal structure of a flexagon.

Flex notation

Recall the flex notation that has been used to describe a series of flexes relative to the current vertex. Here’s what we’ve defined so far:

• > : shift the current vertex one vertex clockwise
• < : shift the current vertex one vertex counterclockwise
• ^ : turn the flexagon over, keeping the same current vertex
• F : perform a flip flex
• P : perform a pinch flex
• S : perform a pyramid shuffle
• St : perform a silver tetra flex
• T : perform a tuck flex; also T1, T2, etc. to specify additional, required structure
• V : perform a v-flex

Additionally, you can add a ' after a flex symbol to indicate that the flex should be done in reverse, e.g. P' or S'. These symbols can be strung together to describe a series of flexes, e.g. P>>T'^<S.

Generating structure

When the previous chapter showed the minimal flexagon for a given flex, it was using a simple generating sequence in order to create the flexagon.

Consider starting with a hexagon. You can think of this as a degenerate flexagon, one that can’t be flexed at all. What’s the minimal amount of structure necessary you need to add to allow you to perform a pinch flex?

The answer is that every other pat (i.e. stack of triangles in the folded flexagon) needs to have exactly two leaves in it. This gives you the 9-triangle straight template that folds into the 3-faced hexaflexagon. (Recall that the large numbers go on the front of the template and the small numbers on the back.)

You can express the concept of creating exactly the structure necessary to perform a flex by adding either a * or + to a flex symbol.* means that you add the structure and perform the flex, while + means that you add the structure without performing the flex. Thus, the 3-faced hexaflexagon has a generating sequence of P* or P+. The difference isn’t important when it’s just a single flex, but becomes more important when there are a series of flexes.

So let’s look again at the minimal hexaflexagon for some of the flexes. Pick a button with a generating sequence on it to see the resulting folded flexagon with its structure (represented by -, [- -], [[- -] -], etc.), followed by the unfolded template.

P+,S+,T+,V+.

Pinch flex sequences

Let’s now do something a bit more interesting: try to figure out generating sequences that can give us the 4, 5, 6, 7, and 8 faced flexagons from the flexagon intro chapter.

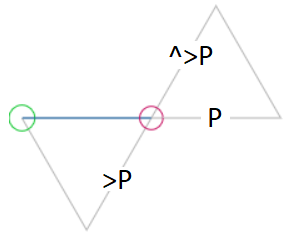
First, let’s get a feel for how different flexes travel around the pinch flex state diagram that we saw in that chapter. Let’s say we’ve done a pinch flex, taking us from the green circle in the adjacent diagram to the red circle.

We can now step in one of four directions, depending on what we do next:

• If we do another pinch flex (P) at the same corner, it’ll take us another step in the same direction, traveling along the adjacent triangle.
• If we instead shift the current vertex one to the right before doing a pinch flex (>P), we’ll step clockwise around the same triangle.
• If we turn over the flexagon, shift one vertex to the right, and then do a pinch flex (^>P), our path will take a slight left turn onto the adjacent triangle.
• If we do the pinch flex in reverse (P') or turn over the flexagon and do a pinch flex (^P), we return back to where we started

The one other thing to know is that once you travel along a single edge of a triangle in the pinch flex state diagram, all the structure necessary to allow you to pinch flex along any of the other edges of that triangle must be present.

Put those facts together, and that means that applying the generating sequence P*P* will create exactly those two triangles in the above diagram. Alternately, you could use P*^>P* to accomplish the same thing. However, P*>P* will not, because it only travels along the first triangle, not the second. Since we’ve been looking at the state diagram for the 4-faced flexagon, this tells us that either of the generating sequences P*P* or P*^>P* can be used to create it.

I’ll give you one more example before letting you try on your own. The diagram to the right is for the 7-faced variant C flexagon. The blue line shows the track that the flex sequence P*P*P*^>P*P* takes through the diagram, starting at the green circle and ending at the red circle. Since it contains an edge of every triangle, it’s one possible generating sequence for that flexagon. And since it only contains a single edge of each triangle, it’s the shortest possible generating sequence, though it’s not unique.

You should now know enough to be able to figure out your own generating sequences by looking at a pinch flex diagram. Below are the state diagrams for all of the 5, 6, and 7-faced flexagons.

Try creating each of those diagrams by typing in a generating sequence using any of >, <, ^, P, and P*. What’s the shortest sequence for each diagram? What if you include P+ (the equivalent of P*P')?

Generating sequence:

If you would like to try more, here are the pinch flex diagrams for all of the 8-faced flexagons:

General generating sequences

This final section gives you the freedom to try out generating sequences that consist of any of the other flexes we’ve discussed. And you can try them on lots of different triangle flexagons. Type in a sequence and explore the resulting flexagon, both the simulated version and a real one, by cutting out and assembling the templates below. Note that not all flexes are available on all flexagons.

Flexes to try: ^, >, <, P*, S*, F*, T*, T1*, V*, St*, or P+, etc.

Generating sequence: apply

Template:

What next?

That last section should give you lots to experiment with. Being able to switch between a wide variety of triangle flexagons and type in arbitrary flex sequences could keep you occupied for a long time. Even fairly simple flexagons can have a huge number of states when you apply several types of flexes to it. How many states are there in a given flexagon? Can you reach them all? Can you figure out how to get back to where you started? Can you find new flexes that open up even more possibilities?

Return to the Table of Contents.