
|
The dodecaflexagon has 12 triangles meeting in the center. Dodecaflexagons are particularly interesting because of the rich symmetry and the wide variety of possible flexes. Three variants are described here:


Isosceles DodecaflexagonCut out the net and pre-crease all the edges. Copy the small numbers on to the back. With the 3 sided version, fold 2 on 2 and tape the tabs to the appropriate faces. 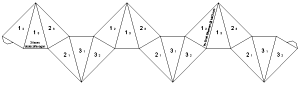
With this 5 sided version, cut out both pieces and tape 1/2 on the top strip to 4/3 in the bottom strip to make one long strip. Fold 4 on 4, 3 on 3 and 2 on 2. Tuck the final pair of 2's together so you have a dodecagon with all 0's on one side and 1's on the other. In the video above, the 0's have been colored red, 1 is green, 2 is gray, 3 is blue and 4 is purple. Note that not all flexes can be done in all positions. 
This 5-sided version is especially interesting because of all the possible flexes. You can do a pinch flex with either 3-fold or 6-fold symmetry. Pocket flexes are possible in many places. The pyramid shuffle and tuck flex can be used to mix up the faces. Or the slot flex can be used to thoroughly mix things up. 
Bronze DodecaflexagonThe bronze dodecaflexagon is made from bronze (30-60-90) triangles. Due to the many symmetries - 2-fold, 3-fold, 4-fold, 6-fold and 12-fold - the variety of flexes possible with this one is quite rich. Follow similar directions as above to make the 3 sided bronze dodecaflexagon. 
While there's only a single 4-sided hexaflexagon made from equilateral triangles, there are three different 4-sided bronze dodecaflexagons. For each of the following strips, cut along the solid black lines and fold along the dashed gray lines. For the star, fold 4 on 4 and 3 on 3. For the ring, fold 4 on 4 and 2 on 2. For the spiral, start by aligning the two hexagons on top of each other, printed side up. Tape 1/3 to 4/2 to connect the two hexagons. Fold 3 on 3 and 2 on 2. When finished folding each one, tape the first and last triangles together along their short edge. 

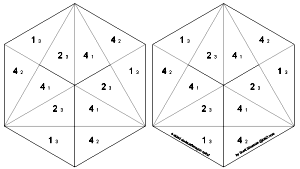
There are many interesting flexes on these 4-sided dodecaflexagons. As with the isosceles version, you can do a pinch flex with either 3-fold or 6-fold symmetry. From the spiral, you can use the silver tetra flex to change just 4 leaves on each side (e.g. from side 4 with side 1 on the back). Or, from the same position, you can use the single flap flex to change just 2 leaves on each side. 
More information on the right triangle version can be found on pages by Ann Schwartz at http://www.eighthsquare.com/12-gon.html and Robin Moseley at http://www.flexagon.net/index.php?option=com_content&task=view&id=16&Itemid=30. Star Dodecaflexagon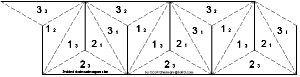
Cut along the solid lines and pre-fold along the dashed lines. The dashed lines along the outside edge of triangles 3/1 and 3/2 indicate that these edges will be connected to each other. Copy the small numbers onto the backs of the triangles. Fold each pair of adjacent 3's together so you have a 6 pointed star. Tape the first and last triangles together, leaving you with all 1's on one side and all 2's on the other. Like the other dodecaflexagons, the star dodecaflexagon has lots of rich symmetry that makes for interesting flexes. You can use the same pivot flex you use on the other star flexagons, but you can do it in many places. There are two different ways to fold it in half or in thirds (like a pinch flex), both of which may allow multiple pivot flexes. Sometimes this takes you to new faces and sometimes this mixes up the faces. To flex the 3-sided version, start with side 2 facing you. Fold it in half through the middle of two of the points. You should see three chevrons (pairs of triangles) with their points meeting. Lift the tip of the left-most chevron and pull it up and to the left. It should pivot smoothly over a saddle point between four triangles of 3ís before folding flat with the chevron pointing down. Now lift the middle tip and do the same thing, pivoting a set of triangles with 3ís on them. Finally, do the same thing with the last chevron, pulling it back and to the right. You should now be able to open the half-star back out flat to reveal all 3ís on one side and 1ís on the other. 
This 5-sided star dodecaflexagon is a little trickier to make. Cut out the six pieces along the solid lines. The dashed line along one side of the 1/5 triangle indicates it will be attached to another triangle later. Pre-fold along the dotted lines. Copy the small numbers onto the backs of the triangles. 
Note that each of the six pieces starts with a triangle labeled 1/5 and ends with one labeled 3/2. Eventually the shortest free edge of the 3/2 will be connected to the shortest free edge of the 1/5 in the next piece, with all the pieces connected in a loop. Start with one piece. Take another piece and turn it over. Tape the short free edge of the 3/2 triangle to the short free edge of the 5 (the other side of the triangle is a 1). Take the next piece and tape the 1 of 1/5 to the 2 in 3/2. Continue in this fashion, taping 3 to 5 then 1 to 2 until all six pieces are chained together. To fold the flexagon, start at the end labeled 3/2. Fold the adjacent 4ís together, then the adjacent 5ís and adjacent 3ís. This may require a bit of twisting and bending. Continue in this manner down the chain, 4 on 4, 5 on 5 and 3 on 3 till you have a star. Tuck the final 3ís together so you have all 1ís on one side and 2ís on the other. Tape the final 1/5 and 3/2 together on their short outside edges. The same 3-chevron-pivot flex works on the 5-sided version, but there are some new possibilities as well. Start on side 1 and fold it in half through the V between tips of the star. You can now perform the chevron-pivot flex in two places instead of the three you get when you fold it in half through the points. When you open it back out flat, one side will have eight 4ís and four 1ís while the other will have eight 2ís and four 3ís. With a bit of experimentation, you should be able to find all five sides, both mixed up and solid. 
You can also fold it using 3-fold symmetry, pivot and open it back up in various ways. 
|
