The Pentadecahexaflexagon

The following diagrams illustrate the Tuckerman traverse for a 15-sided hexaflexagon made from a straight strip of triangles. Here are 4 different ways to fold the strip and diagrams of the corresponding Tuckerman traversal.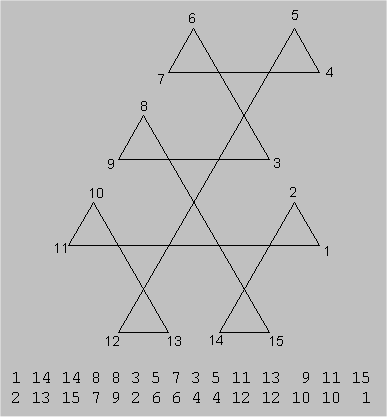

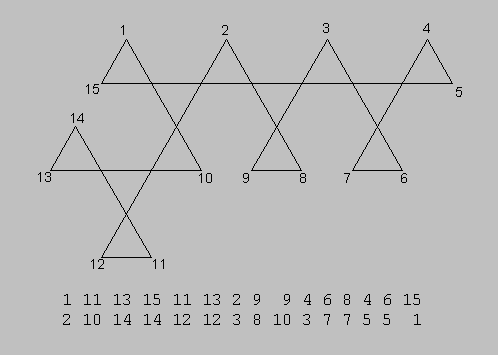
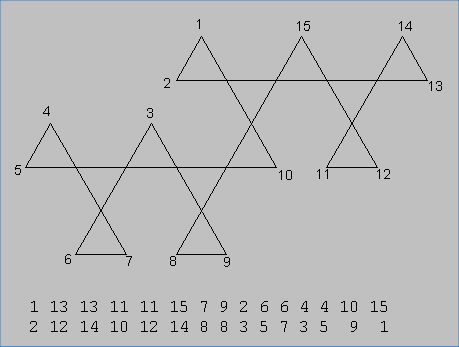
This last diagram would overlap itself so to make it clearer, I extended several lines. The extensions are marked in red.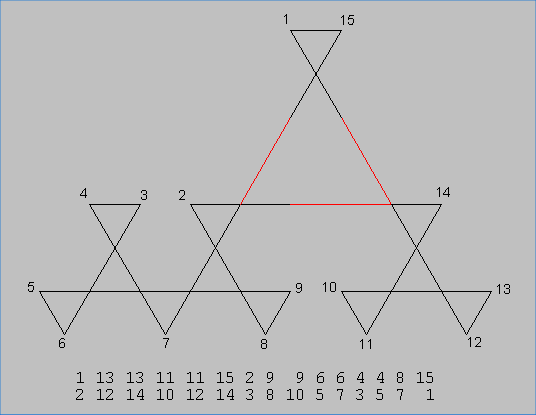

The following is the complete list of all 14 variations for the 15-sided hexaflexagon:

1 12 10 14 12 10 15 15 6 4 2 6 4 9 7
2 11 11 13 13  9  1 14 7 3 3 5 5 8 8

1 14 10 10 12 12 15 15 4 4 6 6 2 9 7
2 13 11  9 13 11  1 14 5 3 7 5 3 8 8

1 3 14  1 5 9  9 7 7 4 4 13 13 11 11
2 2 15 15 6 8 10 6 8 3 5 12 14 10 12

1 3 10 12 5 9  9 7 7 15 15 13 13 4 4
2 2 11 11 6 8 10 6 8 14  1 12 14 3 5

1 10 10 8 8 12 4 6 2 4 6 15 15 13 13
2  9 11 7 9 11 5 5 3 3 7 14  1 12 14

1 3 12 14 10 12 14 8 8 6 6 10 15 4 4
2 2 13 13 11 11 15 7 9 5 7  9  1 3 5

1 3 13 15 8 12 12 10 10  1 5 7 3 5 7
2 2 14 14 9 11 13  9 11 15 6 6 4 4 8

1 3 13 15 10 12 8 10 12  1 5 7 3 5 7
2 2 14 14 11 11 9  9 13 15 6 6 4 4 8

1 3 8 15 15 10 12 14 10 12 5 7 3 5 7
2 2 9 14  1  9 13 13 11 11 6 6 4 4 8

1 3 8 15 15 12 12 10 10 14 5 7 3 5 7
2 2 9 14  1 11 13  9 11 13 6 6 4 4 8

1 3 13 15 11 13 15 6 8 10 6 8 3 5 10
2 2 14 14 12 12  1 5 9  9 7 7 4 4 11

1 3 13 15 11 13 15 4 6 10 10 8 8 5 5
2 2 14 14 12 12  1 3 7  9 11 7 9 4 6

1 11  9 14 12  1 14 12 3 3 6 6 8 8 4
2 10 10 13 13 15 15 11 4 2 7 5 9 7 5

1 11  9  1 12 12 14 14 3 3 8 6 4 8 6
2 10 10 15 13 11 15 13 4 2 9 5 5 7 7

The sequence of how many different hexaflexagon variations can be folded from a straight strip can be found at http://www.research.att.com/~njas/sequences/A007282